
TECHNICAL BLOG
Error-detected coherence metrology of a dual-rail encoded fixed-frequency multimode superconducting qubit
- OQC’s novel dual-rail dimon qubit, the DDQ, demonstrates reproducible high-quality error-detected qubits through targeted suppression of physical qubit error. Such error-detection at the individual qubit level brings the scaling requirements for fault tolerance within reach.
- The encoded qubits exhibit significantly improved bit-flip and phase-flip error rates, with lifetimes exceeding 1 ms and stable over the course of 50 hours.
- The encoding method used has unique sensitivities to noise and sources of decoherence, and can be a useful tool to further understand and address noise sources in our qubits to inform future work.
- This work demonstrates that through intentional design superconducting qubits can be made significantly more robust with minimal increase to their size and complexity. The dual-rail dimon qubit enables OQC’s strategy for hardware-efficient quantum error correction to realise rapidly scalable, low-error quantum computation, forming the basis of our roadmap to 2035.

James Wills
SENIOR QUANTUM ENGINEER
James completed his PhD in Physics at the University of Oxford, in the group of Peter Leek. He worked on the design, simulation, and measurement of novel coaxial qubits, specialising in multi-mode coaxial transmons for quantum computing and sensing applications. He joins OQC as a Quantum Engineer, working in the Quantum Research and Development team.

Mohammad Tasnimul Haque
QUANTUM ENGINEER
Mohammad Tasnimul Haque is a quantum engineer specialising in superconducting quantum circuits, cryogenic measurements, and quantum transport. He currently works in our Quantum Science and Exploratory Research group, where he focuses on qubit calibration, benchmarking, and optimising cryogenic measurement systems for high-fidelity quantum operations. Prior to this, he served as a Doctoral Researcher at Aalto University’s Low Temperature Laboratory in Finland, where he investigated superconducting quantum circuits with graphene Josephson junctions under the supervision of Prof. Dr. Pertti Hakonen.

Brian Vlastakis
VP OF QUANTUM SCIENCE & EXPLORATORY RESEARCH
Brian is VP of Quantum Science & Exploratory Research at OQC. Originally from the United States, Brian moved to the UK in 2017 where he has served as a Marie Curie research fellow at the University of Oxford focusing on superconducting quantum circuits. Previously a research staff scientist for IBM, Brian helped develop their large-scale quantum computing platform. He was also a part of the founding team for the ‘IBM Quantum Experience’, the first publicly-accessible quantum computer. Brian received his PhD in experimental physics at Yale University with work that showed the largest ‘Schrodinger cat states’ to date using microwave photons.
Today, current generation quantum computers are restricted in the usefulness of their computational power due to limiting factors such as physical error rates, decoherence times, hardware limitations, and number of qubits. Across academia and industry alike, it is now generally expected that the first commercial applications of quantum computing will be realised when a quantum computer can run millions of reliable quantum operations, known as MegaQuop.
To reach this milestone, physical qubit numbers alone will not tell the complete story of a quantum device’s performance. We need to reduce errors. At OQC, we focus on hardware-efficient error reduction strategies, building logical qubits that enable the detection and suppression of the most prevalent errors.
Understanding logical qubits
Quantum error-correction (QEC) is the process of encoding a single bit of quantum information (logical qubit) across an array of noisy physical data qubits. We use ancillary qubits, or flags, to determine when and where errors occur in the data qubits, and provide correction pulses to retain the logical qubit state at an error-rate lower than the constituent physical qubits. This requires the ability to detect and correct errors faster than they occur. A major challenge in QEC is that this process only works when the physical error rates are below an error threshold, determined by the particular encoding method used.
Existing error correction schemes can often require 1000s of physical qubits with errors of less than 1% in order to reach the required logical error-rates needed for useful quantum computation. The scale of this can drastically increase hardware overheads and introduce further complexities for control wiring and cryogenic infrastructure, impacting the speed at which companies can scale their devices.
Unlocking hardware efficient error detection
OQC developed its industry-leading dual-rail encoded qubit design, the DDQ, which fits within our proprietary, existing Coaxmon™ architecture. Research carried out by OQC’s team last year demonstrated the DDQ as a hardware efficient method for reducing the most significant source of error in our quantum computers. The work demonstrated a unit-cell of hardware-efficient quantum error detection in coaxial architecture and showed improvements in bit flip and phase flip errors.
Learn more about why we need error correction, our unique approach to the dual-rail dimon qubit, and the dauntingly large cost implication of error correction through hardware advancements alone, in our blog on ‘Hardware efficient error-detection’.
OQC’s latest research in error-detection
This latest research carried out by OQC’s team, now available on arXiv, builds on our hardware efficient error-detection technique and our DDQ design. The work showcases a multi-qubit demonstrator of the technology and outlines a clear path for our architecture to maintain quality and stability while scaling up, demonstrating that through intentional design, superconducting qubits can be made significantly more robust with minimal increase to their size and complexity.
Error-detected logical qubits
In this research, we demonstrate the encoding of an error-detected logical qubit in a fixed-frequency multimode transmon qubit, using dual-rail encoding. While a conventional transmon qubit generally has two superconducting islands and one Josephson junction, the multimode transmon consists of three superconducting islands, and two Josephson junctions. This additional island and junction adds a degree of freedom to the circuit, and subsequently a second transmon-like mode.
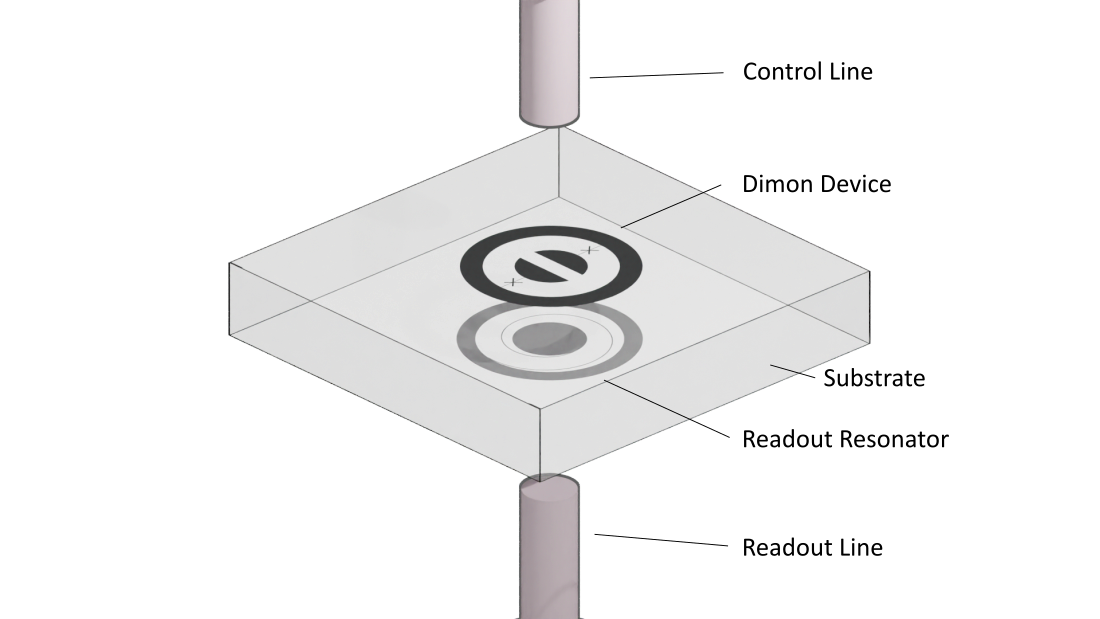
Figure 1. Schematic of the multimode qubit in a coaxial circuit QED architecture unit-cell.
The device is constructed in a coaxial architecture, where the device, control, and readout circuitry occupies the same physical footprint of the conventional coaxial qubit with each mode being addressed via the same coaxial control line and manipulated via a microwave signal. This extensible architecture therefore increases the functionality of the Coaxmon™ unit-cell whilst negating the need for ancillary control wiring or circuit components.
Our architecture incorporates error-detection and potential for correction capabilities at the single qubit level to boost performance in the form of the dual-rail encoded dimon qubit (DDQ). The DDQ, an individual logical qubit, can then form the inner component of a larger concatenated code. Concatenation of error-correction and detection methods allow us to make a logical qubit from an array of smaller logical qubits, that perform better than any physical qubit we can make.
Using this individual qubit-level error detection and suppression capability, the DDQ forms an individual high-quality qubit and significantly relaxes the physical error-thresholds required for quantum error correction; bringing the scaling requirements for fault tolerance within reach. This can also drastically reduce the hardware overheads required to reach certain target logical error-rates, reducing the infrastructure requirements and forming the foundation for the OQC roadmap to TeraQuop devices.
The research
Amplitude damping and removing its effects
The research focuses on a dominant source of error in high performance quantum processors: amplitude damping, which is characterised by the decay constant conventionally known as T1.
What is qubit T1?
A qubit’s T1 is its energy relaxation rate, referring to the process of a qubit to change from a |1⟩ state to a |0⟩ state. It is a specific type of loss where a qubit loses energy, causing it to decay from its excited state and return to its ground state.
The implementation for our promising error-detection approach with dual-rail encoding, can be used to efficiently detect when an error has occurred. When an energy relaxation event of the physical qubit modes takes place, a detectable leakage occurs outside of the computational subspace, signalling the occurrence of an error. This activity forms an integral part of identifying and addressing when/where an error has occurred.
The work demonstrates protocols for reading out the logical state and performing an end-of-line (EOL) error detection. The EOL readout method used allows us to perform a number of experiments using the logical encoding of the DDQ, and detect the shots in which there has been leakage outside of the computational subspace. We can remove this fraction of results by a postselection process which allows us to obtain the error-detected logical state probabilities. This in turn lets us remove the effects of the physical qubit’s T1 on the logical qubit computations, and greatly improves the performance of the hardware in use as a quantum memory.
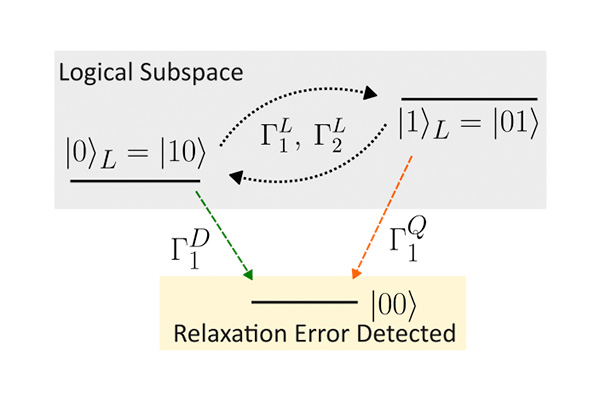
Figure 2. Energy level diagram of the dimon device, highlighting the logical subspace and relaxation error-detected states. Orange (green) arrows indicate energy level transitions, and labelled transition rates, following relaxation events of the dimon quadrupole (dipole) mode.
The research results
Through the process of error-detection and postselection, we show how bit-flip and phase flip error rates in the logical subspace are greatly reduced in comparison to the constituent physical modes of the device. Where a conventional measurement of a superconducting qubit relaxation (or T1 decay) typically shows an exponential decay, the logical bit-flip measurement shows a more complex second-order type decay profile, since the first order decay events are removed via the encoding and error-detection process. Similarly, we observe a non-exponential decay in the error-detected measurement of the logical phase-flip metrics.
In short time-scales, we see these error-detected coherence metrics improve by an order of magnitude over the physical modes of the DDQ. If a conventional transmon qubit were to show the same bit-flip error rate, it would have to have a T1 of over 1 ms, on a level with some of the best superconducting qubit hardware platforms ever developed. These time scales and low error-rates are significant for quantum algorithms and quantum error-correction cycles, offering the potential for profound increases in algorithmic fidelity, as well as reductions in physical hardware overheads for quantum error correction. Stability and repeatability are important features for components of quantum processors, and we demonstrate the error-rates remain low over the course of 50 hours, across an array of three DDQ devices.
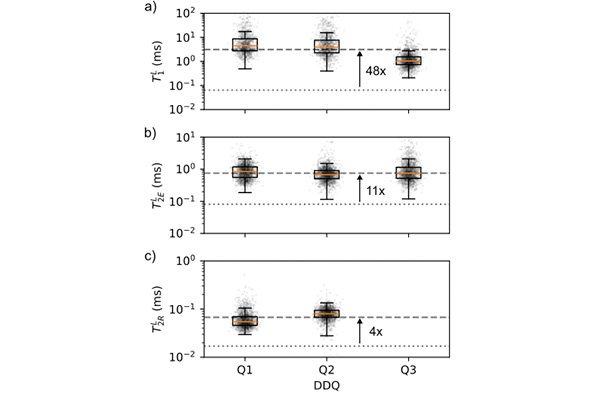
Figure 3. Logical coherence metric distributions.
In addition, this method of encoding a qubit in a multimode structure has unique sensitivities to noise and sources of decoherence. By repeatedly measuring frequency deviations in the physical and logical subspace, and performing noise analysis, we are able to obtain more information about the physical sources of decoherence in our system. The DDQ has a unique utility as an extremely sensitive detector, and can be a useful tool in investigations into the fundamentals of materials and nanofabrication methodologies in superconducting qubits. For future generation qubits to overcome current limitations and operate with significantly reduced error rates, understanding these noise sources is crucial. The results produced and validated across multiple devices, supports a significant step in demonstrating the viability of the platform used for future hardware integrations.
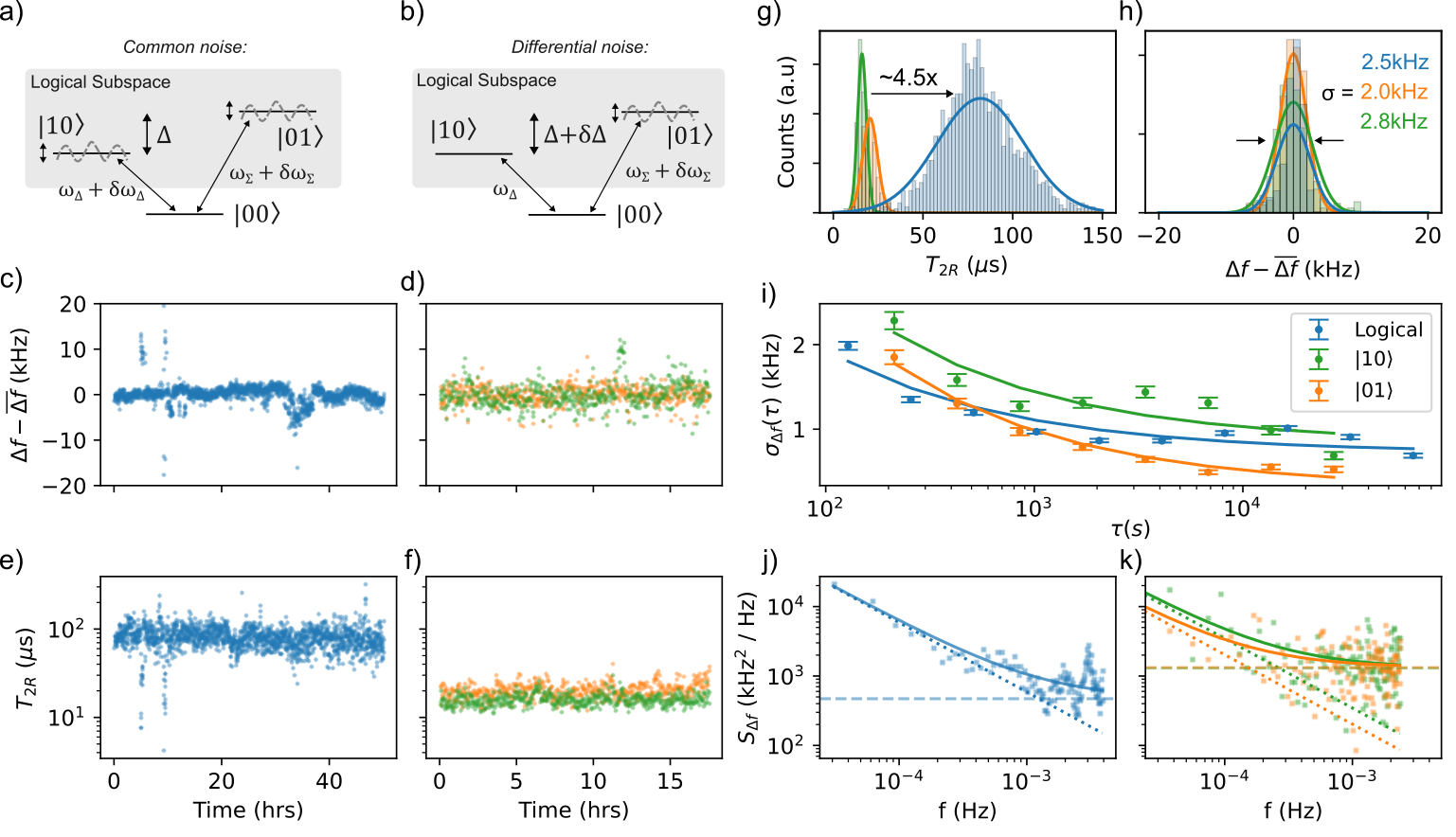
Figure 4. Ramsey interferometry measurements of logical encoded qubit, and physical modes of Q2.
Moving from the physical to the logical era
The novel research carried out marks an important point on the path to reaching useful quantum computation. Not only does the research demonstrate capability and understanding of QEC with error-detection, but it also provides a hardware efficient method in which to scale to the physical qubit numbers required for useful quantum computation. This architecture therefore has the potential to fundamentally change the economics of quantum computing by reducing the infrastructure and hardware costs needed to achieve commercially-useful quantum computation.
Additionally, the error-detected QPU hardware platform used has capabilities of running useful quantum algorithms, supporting the benchmarking of quantum algorithms and producing industry level performance on the hardware.
The dual-rail dimon qubit technology, the DDQ, used in this research, enables OQC’s strategy for hardware-efficient quantum error correction to realise rapidly scalable, low-error quantum computation, and forms the basis of our roadmap to 2035.
Read the full preprint on ArXiv.
Error-detected coherence metrology of a dual-rail encoded fixed-frequency multimode superconducting qubit.
James Wills, Mohammad Tasnimul Haque, Brian Vlastakis
Join our newsletter for more articles like this
By clicking ‘sign up’ you’re confirming that you agree with our Terms & Conditions


